Rangkaian Arus Bolak Balik, Listrik, Daya, Resonansi, Pengertian, Fungsi, Resistor, Induktif, Kapasitor, Seri RLC, Rumus, Contoh Soal, Jawaban, Praktikum, Penerapan, Aplikasi

Dalam kehidupan sehari-hari kita jumpai alat-alat seperti dinamo sepeda
dan generator. Kedua alat tersebut merupakan sumber arus dan tegangan
listrik bolak-balik. Arus bolak-balik atau alternating current (AC)
adalah arus dan tegangan listrik yang besarnya berubah terhadap waktu
dan dapat mengalir dalam dua arah. Arus bolakbalik (AC) digunakan secara
luas untuk penerangan maupun peralatan elektronik. Dalam bab ini kita
akan membahas mengenai hambatan, induktor, dan kapasitor dalam rangkaian
arus bolak-balik.
 |
| Gambar 1. Setrika merupakan alat yang menggunakan arus listrik bolak balik. [1] |
Sumber arus bolak-balik adalah generator arus bolak-balik yang prinsip
kerjanya pada perputaran kumparan dengan kecepatan sudut ω yang berada
di dalam medan magnetik. Sumber ggl bolak-balik tersebut akan
menghasilkan tegangan sinusoida berfrekuensi f. Dalam suatu rangkaian
listrik, simbol untuk sebuah sumber tegangan gerak elektrik bolak-balik
adalah :
Tegangan sinusoida dapat dituliskan dalam bentuk persamaan tegangan sebagai fungsi waktu, yaitu:
V = Vm.sin
2π.f.t .................................................. (1)
Tegangan yang dihasilkan oleh suatu generator listrik berbentuk
sinusoida. Dengan demikian, arus yang dihasilkan juga sinusoida yang
mengikuti persamaan:
I = Im.sin
2π.f.t .................................................... (2)
dengan Im adalah arus puncak dan t adalah waktu.
Untuk menyatakan perubahan yang dialami arus dan tegangan secara
sinusoida, dapat dilakukan dengan menggunakan sebuah diagram vektor yang
berotasi, yang disebut diagram fasor. Istilah fasor menyatakan vektor
berputar yang mewakili besaran yang berubah-ubah secara sinusoida.
Panjang vektor menunjukkan amplitudo besaran, dan vektor ini dibayangkan
berputar dengan kecepatan sudut yang besarnya sama dengan frekuensi
sudut besaran. Sehingga, nilai sesaat besaran ditunjukkan oleh
proyeksinya pada sumbu tetap. Cara ini baik sekali untuk menunjukkan
sudut fase antara dua besaran. Sudut fase ini ditampilkan pada sebuah
diagram sebagai sudut antara fasor-fasornya.
Materi Fisika :
Generator pada pusat pembangkit listrik modern tidak menghasilkan
listrik pada tegangan tinggi yang mencukupi untuk transmisi yang
efisien. Tegangan dinaikkan dengan transformator step-up supaya
transmisi jarak jauh menjadi efisien.
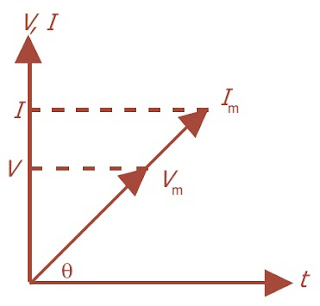 |
| Gambar 2. Diagram fasor arus dan tegangan berfase sama. |
Gambar 2. memperlihatkan diagram fasor untuk arus sinusoida dan tegangan
sinusoida yang berfase sama yang dirumuskan pada persamaan (1) dan (2).
Ketika di kelas X kita telah mempelajari dan mengetahui bahwa:
yang menyatakan akar kuadrat rata-rata tegangan. Dan akar kuadrat rata-rata arus, yang dirumuskan:
Nilai rms dari arus dan tegangan tersebut kadang-kadang disebut sebagai “nilai efektif ”.
1. Rangkaian Resistor
Gambar 3(a) memperlihatkan sebuah rangkaian yang hanya memiliki sebuah elemen penghambat dan generator arus bolak-balik.
Karena kuat arusnya nol pada saat tegangannya nol, dan arus mencapai
puncak ketika tegangan juga mencapainya, dapat dikatakan bahwa arus dan
tegangan sefase (Gambar 3(b)). Sementara itu, Gambar 3(c) memperlihatkan
diagram fasor arus dan tegangan yang sefase. Tanda panah pada sumbu
vertikal adalah nilai-nlai sesaat. Pada rangkaian resistor berlaku
hubungan:
 |
| Gambar 3. (a) Rangkaian dengan sebuah elemen penghambat (b) Arus berfase sama dengan tegangan (c) Diagram fasor arus dan tegangan. |
VR = Vm .sin 2π .f.t
VR = Vm .sin ωt ....................................................... (5)
Jadi,
IR = VR/R = (Vm/R) sin
ωt
IR = Im.sin ωt ......................................................... (6)
Dalam rangkaian AC seperti yang diperlihatkan pada gambar, R = 40Ω, Vm = 100 V, dan frekuensi generator f = 50 Hz. Dianggap tegangan pada ujung-ujung resistor VR = 0 ketika t = 0. Tentukan:
a. arus maksimum,
b. frekuensi sudut generator,
c. arus melalui resistor pada t = 1/75 s
d. arus melalui resistor pada t = 1/150 s
Penyelesaian:
a. Rangkaian resistor murni, Im dapat dicari dengan persamaan:
Im = Vm/R = 100/40 = 2,5 A
b. Frekuensi sudut anguler (ω)
ω = 2. π .f = 2. π .50 = 100 π
c. Untuk rangkaian resistor murni, tegangan sefase dengan arus, sehingga untuk V = Vm.sin ωt, maka I = Im.sin ωt. Persamaan arus sesaat yaitu:
2. Rangkaian Induktif
 |
| Gambar 4. (a) Rangkaian induktif (b) Arus berbeda fase dengan tegangan (c) Diagram fasor arus dan tegangan yang berbeda fase. |
Gambar 4. memperlihatkan sebuah rangkaian yang hanya mengandung sebuah
elemen induktif. Pada rangkaian induktif, berlaku hubungan:
Tegangan pada induktor VL setara dengan tegangan sumber V, jadi dari persamaan (9) dan (10) akan diperoleh:
maka,
Jika ωL = 2π fL didefinisikan sebagai reaktansi induktif (XL), maka dalam suatu rangkaian induktif berlaku hubungan sebagai berikut:
Perbandingan persamaan (10) dan (12) memperlihatkan bahwa nilai VL dan IL yang
berubah-ubah terhadap waktu mempunyai perbedaan fase sebesar seperempat
siklus. Hal ini terlihat pada Gambar 4(b), yang merupakan grafik dari
persamaan (10) dan (12).
Dari gambar terlihat bahwa VL mendahului IL, yaitu dengan berlalunya waktu, maka VL mencapai maksimumnya sebelum IL mencapai
maksimum, selama seperempat siklus. Sementara itu, pada Gambar 4(c),
pada waktu fasor berotasi di dalam arah yang berlawanan dengan arah
perputaran jarum jam, maka terlihat jelas bahwa fasor VL,m mendahului fasor IL,m selama seperempat siklus.
Sebuah induktor 0,2 henry dipasang pada sumber tegangan arus
bolak-balik, V = (200. sin 200t) volt. Tentukan persamaan arus yang
mengalir pada rangkaian tersebut!
Penyelesaian:
Diketahui:
V = (200 sin 200t) volt
L = 0,2 H
Ditanya: I = ... ?
Pembahasan :
V = Vm.sinωt
V = 200.sin 200t
Dari persamaan diketahui Vm = 200 volt dan ω= 200 rad/s, maka:
XL = ω.L= (200)(0,2)
XL = 40Ω
Gambar 6. memperlihatkan sebuah rangkaian yang hanya terdiri atas sebuah
elemen kapasitif dan generator AC. Pada rangkaian tersebut berlaku
hubungan:
Vc = V = Vm.sin
ωt ................................................. (15)
Dari definisi C diperoleh hubungan bahwa VC = Q/C, maka akan diperoleh:
Q = C.Vm.sin ωt
atau
IC = dQ/dt =
ω.C.Vm.cos ωt ...................................... (16)
maka akan diperoleh:
Jika didefinisikan sebuah reaktansi kapasitif (XC), adalah setara dengan 1/ω.C atau 1/2 π.f.C, maka dalam sebuah rangkaian kapasitif akan berlaku hubungan sebagai berikut:
Persamaan (15) dan (16) menunjukkan bahwa nilai VC dan LC yang berubah-ubah terhadap waktu adalah berbeda fase sebesar seperempat siklus. Hal ini dapat terlihat pada Gambar 6(b), yaitu VC mencapai maksimumnya setelah IC mencapai
maksimum, selama seperempat siklus. Hal serupa juga diperlihatkan pada
Gambar 6(c), yaitu sewaktu fasor berotasi di dalam arah yang dianggap
berlawanan dengan arah perputaran jarum jam, maka terlihat jelas bahwa
fasor VC,m tertinggal terhadap fasor IC,m elama seperempat siklus.
 |
| Gambar 6. (a) Rangkaian kapasitif (b) Perbedaan potensial kapasitor terhadap arus (c) Diagram fasor rangkaian kapasitif. |
Contoh Soal 2 :
Sebuah kapasitor 50 μF dihubungkan dengan sumber tegangan arus
bolak-balik. Arus yang mengalir pada rangkaian adalah I = (4.sin 100t)
A. Tentukan persamaan tegangan pada kapasitor itu!
Penyelesaian:
Diketahui:
C = 50 μF = 5 × 10-5 F
I = (4.sin 100t) A
Ditanya: Persamaan tegangan, V = ...?
Pembahasan :
I = (Im.sin ω ) A
I = (4.sin100t) A
Percobaan Sederhana / Praktikum Fisika 1 :
Tujuan : Mengetahui rangkaian kapasitor dan listrik bolak-balik.
Alat dan bahan : Trafo adaptor, kabel penghubung, kapasitor, amperemeter, voltmeter, dan CRO.
- Rangkailah alat dan bahan secara seri sesuai gambar.
- Bacalah nilai beda potensial pada kapasitor dengan voltmeter yang tersedia.
- Gambarkan bentuk VC yang ditampilkan oleh CRO.
- Bacalah nilai beda potensial pada kapasitor dengan CRO yang tersedia.
- Carilah harga efektif berdasarkan pembacaan CRO.
- Ulangilah langkah 2 - 4 untuk berbagai jenis kapasitor berdasarkan kapasitasnya.
- Carilah harga impedansi induktor bilamana f = 60 Hz berdasarkan harga kapasitansi yang tercantum pada kapasitor.
- Catatlah hasil percobaan dengan mengikuti format tabel berikut ini.
Diskusi :
- Gambarkanlah bentuk grafik yang ditampilkan oleh rangkaian kapasitor sederhana sesuai dengan percobaan!
- Berapakah VC efektifnya?
- Apakah nilai XC = 1/2 π.f.C = VC/IR ?
- Tulislah kesimpulan dari percobaan yang telah kalian lakukan!
4. Rangkaian Seri RLC
Pada bagian sebelumnya telah dibahas mengenai rangkaian-rangkaian R, C,
dan L yang dihubungkan terpisah. Maka pada bagian ini kita akan membahas
sebuah rangkaian seri yang di dalamnya terdapat ketiga elemen tersebut,
yang sering disebut rangkaian seri RLC, seperti ditunjukkan pada Gambar
7.
 |
| Gambar 7. Rangkaian seri RLC. |
Berdasarkan persamaan (1), tegangan gerak elektrik untuk Gambar 7. diberikan oleh persamaan:
V = Vm.sin ω .................................................... (20)
Arus (tunggal) di dalam rangkaian tersebut adalah:
I = Im.sin (ω − φ) .............................................. (21)
Dengan ω adalah frekuensi sudut tegangan gerak elektrik bolak-balik pada persamaan (20). Im adalah
amplitudo arus dan φ menyatakan sudut fase di antara arus bolak-balik
pada persamaan (21) dan tegangan gerak elektrik pada persamaan (20).
Pada Gambar 7.7 tersebut akan berlaku persamaan:
V = VR + VC
+ VL .................................................... (22)
Setiap parameter merupakan kuantitas-kuantitas yang berubah-ubah
terhadap waktu secara sinusoida. Diagram fasor yang diperlihatkan pada
Gambar 8. menunjukkan nilai-nilai maksimum dari I, VR, VC, dan VL.
Proyeksi-proyeksi fasor pada sumbu vertikal adalah sama dengan V, seperti yang dinyatakan pada persamaan (22).
 |
| Gambar 8. Diagram fasor yang bersesuain dengan gambar 7. |
Sebaliknya, dinyatakan bahwa jumlah vektor dari amplitudo-amplitudo fasor VR,m, VC,m, dan VL,m menghasilkan sebuah fasor yang amplitudonya adalah V pada persamaan (20). Proyeksi Vm pada sumbu vertikal, merupakan V dari persamaan (20) yang berubah terhadap waktu.
Kita dapat menentukan Vm pada Gambar 9, yang di dalamnya telah terbentuk fasor VL,m - VC,m. Fasor tersebut tegak lurus pada VR,m, sehingga akan diperoleh:
 |
| Gambar 9. Diagram fasor memperlihatkan hubungan antara V dan I pada persamaan 20 dan 21. |
Kuantitas yang mengalikan Im disebut impedansi (Z) rangkaian pada Gambar 7. Jadi, dapat dituliskan:
Im = Vm/Z ............................................................... (24)
Untuk menentukan sudut fase φ di antara I dan V, dapat dilakukan dengan
membandingkan persamaan (20) dan (21). Dari Gambar 7. dapat kita
tentukan bahwa sudut φ dinyatakan:
Pada Gambar 9. menunjukkan nilai XL > XC, yaitu bahwa rangkaian seri dari Gambar 7. lebih bersifat induktif daripada bersifat kapasitif. Pada keadaan ini Vm mendahului Im (walaupun
tidak sebanyak seperempat siklus seperti pada rangkaian induktif murni
dari Gambar 3. Sudut fase φ pada persamaan (26) adalah positif.
Tetapi, jika XC > XL, maka rangkaian tersebut akan lebih bersifat kapasitif daripada bersifat induktif, dan Vm akan tertinggal terhadap Im (walaupun tidak sebanyak seperempat siklus seperti pada rangkaian kapasitif murni).
Berdasarkan perubahan ini, maka sudut φ pada persamaan (26) akan menjadi negatif.
Contoh Soal 3 :
Rangkaian seri RLC, dengan masing-masing R = 30Ω, L = 0,6 H, dan C = 500
μF dipasang pada sumber tegangan bolak-balik dengan V = (200. sin 100t)
volt. Tentukan:
a. impedansi rangkaian,
b. persamaan arus pada rangkaian!
Penyelesaian:
Diketahui:
Rangkaian seri RLC
R = 30Ω ,
L = 0,6 H,
C = 500 μF = 5 ×10-4 F
V = (200.sin 100t) volt
Ditanyakan:
a. Z = ... ?
b. Persamaan I = ... ?
Pembahasan :
a. V = Vm.sin ωt
Vm = 200
V = (200 sin 100t) volt
ω = 100 rad/s
XL = ωt = (100)(0,6) =
60 Ω
b. Im = Vm/Z = 200/40 = 4 A
Contoh Soal 4 :
Hambatan R, induktor L, dan kapasitor C, masing-masing mempunyai nilai
300Ω ; 0,9 H; dan 2 μF . Ketiga komponen listrik tersebut dihubungkan
seri dan diberi tegangan efektif AC sebesar 50 volt dengan kecepatan
sudut 1.000 rad/s. Tentukan:
a. impedansi rangkaian, c. tegangan pada L,
b. arus efektif rangkaian, d. tegangan pada C!
Penyelesaian:
Diketahui:
R = 300 Ω
L = 0,9 H
C = 2 μF = 2 × 10-6 F
Vef = 50 V
ω = 1.000 rad/s
Ditanya:
a. Z = ... ?
b. Ief = ... ?
c. VL = ... ?
d. VC = ... ?
Jawab:
b. Arus efektif
Ief = V/Z = 50 V / 500 Ω = 0,1 A
c. VL = I . XL
= (0,1 A)(900 Ω ) = 90 volt
Percobaan Sederhana / Praktikum Fisika 1 :
Tujuan : Mengetahui rangkaian seri RLC.
Alat dan bahan : Trafo adaptor, kabel penghubung, resistor, induktor, kapasitor, amperemeter, voltmeter, dan CRO.
- Rangkailah sebuah rangkaian seri sesuai dengan gambar di samping.
- Bacalah nilai beda potensial pada resistor, induktor, dan kapasitor dengan voltmeter yang tersedia.
- Gambarlah bentuk grafik VR, VL, dan VC yang ditampilkan CRO.
- Bacalah nilai beda potensial pada resistor, induktor, dan kapasitor dengan CRO yang tersedia.
- Carilah harga efektif berdasarkan pembacaan CRO.
- Ulangilah langkah 2 - 5 untuk berbagai jenis resistor, induktor, dan kapasitor berdasarkan harganya.
- Carilah nilai impedansi rangkaian.
Diskusi :
- Apakah fase dari ketiga beda potensial pada R, L, dan C adalah sama? Mengapa demikian?
- Jelaskan yang dimaksud impedansi rangkaian seri!
- Tulislah kesimpulan dari percobaan yang telah kalian lakukan!
Daya sesaat pada sebuah rangkaian seperti yang terlihat pada rangkaian seri RLC seperti ditunjukkan Gambar 7. dirumuskan:
P(t) = V(t) . I(t)
P(t) = (Vm.sin ωt)(Im.sin (ωt – φ)) .......................... (27)
Jika kita mengekspansikan faktor sin (ωt − φ) menurut sebuah identitas trigonometri, maka diperoleh:
P(t) = (VmIm)(sin ωt )(sin
ωt cos φ – cos ωt sin φ )
P(t) = VmImsin2
ωt cos φ –VmImsin ωt cos ωt sin φ ..... (28)
Nilai sin2ωt = 1/2 dan sin ωt cos ωt = 0, maka dari persamaan (28) kita dapat mencari P(t) = Pav yaitu:
Pav = ½ VmImcos
φ + 0 .......................................... (29)
diketahui :
maka persamaan (29) menjadi:
Pav = Vrms
.Irms cos φ ................................................ (30)
Dengan cos φ menyatakan faktor daya. Untuk kasus seperti pada Gambar 3,
memperlihatkan sebuah beban hambat murni, dengan φ = 0, sehingga
persamaan (30) menjadi:
Pav = Vrms.Irms ...................................................... (31)
Contoh Soal 6 :
Sumber tegangan bolak-balik dengan V = (100 sin1.000t) volt, dihubungkan dengan rangkaian seri RLC seperti gambar. Bila R = 400Ω , C = 5 μF , dan L = 0,5 H, tentukan daya pada rangkaian!
Penyelesaian:
Diketahui:
V = (100.sin 1000t) volt
R = 400Ω
C = 5 μF = 5 × 10-6 F
L = 0,5 H
Ditanya: P = ... ?
Pembahasan :
Menentukan impedansi rangkaian Persamaan umum :
Menentukan impedansi rangkaian Persamaan umum :
V = Vm. sinωt
V = (100. sin 1000t) volt
maka,
Vm = 100 volt
ω = 1.000 rad/s
Kuat arus, I = Vm/Z = 100/500 = 0,2 A
Faktor daya, φ = 400/500 = 0,8
= 37o
C. Resonansi pada Rangkaian Arus Bolak Balik
 |
| Gambar 10. Resonansi dalam rangkaian RLC untuk tiga nilai R berbeda. |
Rangkaian RLC pada Gambar 7. memiliki suatu frekuensi alami dari
osilasi, dan menganggap pada rangkaian tersebut bekerja suatu pengaruh
luar, yang di dalam kasus ini adalah tegangan gerak elektrik bolak-balik
yang diberikan dalam persamaan V = Vm.sin ωt, dengan ω adalah frekuensi sudut dari gaya penggerak. Respons maksimum, Irms, terjadi bila frekuensi sudut ω dari gaya penggerak tersebut persis menyamai frekuensi alami ω0 dari osilasi untuk osilasi bebas dari rangkaian tersebut.
Nilai maksimum Irms terjadi bila XL = XC dan mempunyai:
Irms, maks
= Vrms/R ......................................................... (32)
Irms hanya dibatasi oleh resistansi rangkaian. Jika
R → 0 , Irms, maks → ∞
Nilai  menyatakan sudut alami ω0 untuk rangkaian dari Gambar 7., yaitu nilai Irms maksimum terjadi jika frekuensi ω dari gaya penggerak adalah tepat sama dengan frekuensi alami ω0, yang dinyatakan:
menyatakan sudut alami ω0 untuk rangkaian dari Gambar 7., yaitu nilai Irms maksimum terjadi jika frekuensi ω dari gaya penggerak adalah tepat sama dengan frekuensi alami ω0, yang dinyatakan:
ω = ω0 ................................................................... (34)
Kondisi pada persamaan (34) disebut resonansi. Resonansi pada rangkaian
RLC dari Gambar 7. ditunjukkan oleh Gambar 8, di mana grafik hubungan
Irms terhadap ω untuk nilai-nilai Vm,
C, dan L yang tetap terjadi tetapi untuk tiga nilai R yang berlainan.
Dalam kehidupan sehari-hari kita menerapkan prinsip ini pada saat
menyetel sebuah radio. Dengan memutar kenop (tombol), kita menyesuaikan
frekuensi alami ω0 ari
sebuah rangkaian dalam radio dengan frekuensi ω dari sinyal yang
dipancarkan oleh antena stasiun, sampai persamaan (34) terpenuhi.
Contoh Soal 7 :
Hitunglah frekuensi resonansi dari sebuah rangkaian dengan hambatan yang
diabaikan mengandung induktansi 40 mH dan kapasitansi 600 pF!
Penyelesaian:
Diketahui:
L = 40 mH = 40 × 10-3 H
C = 600 pF = 600 × 10-12 F
Materi Fisika :
Dalam rangkaian sebuah radio penerima, kapasitor dapat berfungsi sebagai
pemilih gelombang radio. Suatu nilai kapasitansi tertentu berhubungan
dengan dengan panjang gelombang radio yang diterima radio. Nilai
kapasitansi pada kapasitor dalam rangkaian sebuah radio dapat diubah.
kapasitor yang memiliki nilai kapasitansi yang dapat diubah disebut
kapasitor variabel.
Referensi :
Budiyanto, J. 2009. Fisika : Untuk SMA/MA Kelas XII. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 298.
Referensi Lainnya :
[1] http://id.wikipedia.org/wiki/Berkas:Electric_iron_lie.jpg
[2] http://en.wikipedia.org/wiki/File:Photo-SMDcapacitors.jpg
[3] http://commons.wikimedia.org/wiki/File:Radio.jpg
Referensi Lainnya :
[1] http://id.wikipedia.org/wiki/Berkas:Electric_iron_lie.jpg
[2] http://en.wikipedia.org/wiki/File:Photo-SMDcapacitors.jpg
[3] http://commons.wikimedia.org/wiki/File:Radio.jpg



































0 komentar:
Posting Komentar